搜索
登录

感应度系数

百科 > 感应度系数

目录

1感应度系数概述 2感应度系数的计算[1]

1.感应度系数概述

感应度系数是指国民经济各部门每增加一个单位最终使用时，某一部门由此而受到的需求感应程度，也就是需要该部门为其他部门生产而提供的产出量。系数大说明该部门对经济发展的需求感应程度强，反之，则表示对经济发展需求感应程度弱。

2.感应度系数的计算[1]

　　(1)

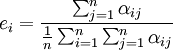
　　e_i=frac{sum_{j=1}^n alpha_{ij}}{frac{1}{n}sum_{i=1}^nsum_{j=1}^nalpha_{ij}}

　　(2)

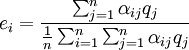
　　e_i=frac{sum_{j=1}^nalpha_{ij}q_j}{frac{1}{n}sum_{i=1}^nsum_{j=1}^nalpha_{ij}q_j}

　　(3)

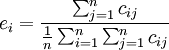
　　e_i=frac{sum_{j=1}^nc_{ij}}{frac{1}{n}sum_{i=1}^nsum_{j=1}^nc_{ij}}

　　(4)

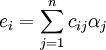
　　e_i=sum_{j=1}^nc_{ij}alpha_j

　　(5)

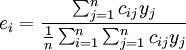
　　e_i=frac{sum_{j=1}^nc_{ij}y_j}{frac{1}{n}sum_{i=1}^nsum_{j=1}^nc_{ij}y_j}

　　(6)

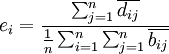
　　e_i=frac{sum_{j=1}^noverline{d_{ij}}}{frac{1}{n}sum_{i=1}^nsum_{j=1}^noverline{b_{ij}}}

　　(7)

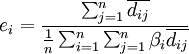
　　e_i=frac{sum_{j=1}^noverline{d_{ij}}}{frac{1}{n}sum_{i=1}^nsum_{j=1}^nbeta_ioverline{d_{ij}}}

　　(8)

　　e_i=sum_{j=1}^nbeta_ioverline{d_{ij}}

　　上述公式中αij为直接消耗系数;qj为j部门的总产出;yj为j部门的最终产出 为;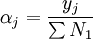alpha_j=frac{y_j}{sum{N_1}}为j部门的最终产出占最终产出总量的比例,即最终产出结构系数;cij为完全需求系数;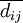overline{d_{ij}}为完全供给系数;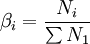beta_i=frac{N_i}{sum{N_1}}为i部门最初投入占最初投入总量的比例,即最初投入结构系数。

评论  |   0条评论
评论