多因素敏感性分析法
1.什么是多因素敏感性分析法
根据不确定性因素每次变动数目的多少,敏感性分析法可以分为单因素敏感性分析法和多因素敏感性分析法。
在单因素敏感性分析中,当计算某特定因素的变动对经济效果指标的影响时,假定其它因素均不变。实际上,许多因素的变动具有相关性,一个因素的变动往往也伴随着其它因素的变动。所以,单因素敏感性分析有其局限性。[1]多因素敏感性分析法是指在假定其它不确定性因素不变条件下,计算分析两种或两种以上不确定性因素同时发生变动,对项目经济效益值的影响程度,确定敏感性因素及其极限值。
多因素敏感性分析一般是在单因素敏感性分析基础进行,且分析的基本原理与单因素敏感性分析大体相同,但需要注意的是,多因素敏感性分析须进一步假定同时变动的几个因素都是相互独立的,且各因素发生变化的概率相同。
多因素敏感性分析要考虑可能发生的各种因素不同变动幅度的多种组合.计算起来要比单因素敏感性分析复杂得多。如果需要分析的不确定因素不超过三个,而且经济效果指标的计算比较简单,可以用解析法与作图法相结合的方法进行分析。[1]
2.多因素敏感性分析法的例子[2]
多因素敏感性分析更为真实地反映了因素变化对经济指标的影响,较常用的有双因素敏感性分析和三因素敏感性分析。
1.双因素敏感性分析
在多个不确定因素中,假定其他因素不变化,仅考虑两个因素变化对经济指标的影响,称为双因素敏感性分析。由于有两个可变因素,所以双因素敏感性分析的图示结果是一个敏感性曲面或区域,以双因素敏感性分析为例说明分析方法。
【例】 设某项目固定资产投资K0 = 170000元,扣除增值税及附加后的年销售净收入S=55000元,年经营成本C=20000元,项目寿命期15年,固定资产残值K_L=17000元。项目要求达到收益率i=15%。试就投资及年净销售收入对该项目的净现值进行双因素敏感性分析。
解:设x表示投资变动的百分比,Y表示年销售净收人变化的百分比,则
NPV(15%)=-170000(1+x)+55000(1+y)(P/A,15%,15)-20000(P/A,15%,15)+17000(P/F,15%,15)
当NPV(15%)≥0时,说明项目的内部收益率为15%或以上,项目是可行的。
NPV(15%)=-170000-170000x+55000×5.8473+55000×5.8473y-20000×5.8473+17000×0.1229=36745-170000x+321602y≥0
或
y≥0.5286x-0.1143
将该不等式绘制在以投资变化率为横坐标,年销售净收入变化率为纵坐标的平面直角坐标系中进行分析(见图1)。
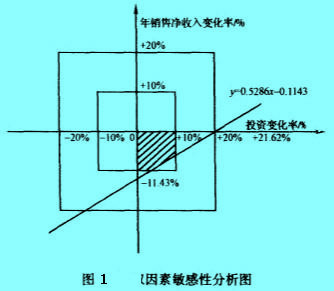
从图1可以看出,斜线y=0.5286x-0.1143把xy平面分为两个区域,斜线上方NPV(15%)>0,项目是可行的;斜线下方NPV(15%)<0,项目是不可行的。若投资及其他因素都不变,只改变年销售净收入,当年销售净收入降低11.43%以上时,项目将由可行变为不可行;若年销售净收入及其他因索不变,当投资额增长21.62%以上时,项目也将由可行变为不可行;若年销售净收入降低与投资增长两因素同时变化,则NPV(15%)≥0的区域在有斜线阴影的区内,项目仍是可行的。
2.三因素敏感性分析
以上仅是两个因素同时变化的敏感性分析,若变化因素多于两个,就比较难以用图形表示。若发生变化的因素扩大到三个,可以将其中一个因素依次改变,就可以得到另两个因素同时变化的一组临界曲线族。
【例】 某投资方案初始投资为100万元,预计项目寿命为5年,每年可提供净收益28万元,基准收益率为8%,项目期末残值为20万元。由于初始投资100万元是估算值,实际上有偏差,而且受物价变化的影响,原材料和燃料动力价格的变化引起预计的年收益也发生变化。若同时考虑基准收益率i为可变因素,试分析这三个因素对净年值的影响。
解:根据题意,净年值为
NAV=28(1+v)+20(A/F,i,5)-100(1+x)(A/P,i,5)
当基准收益率i分别为6%、8%、10%、15%和20%,可得净年值的一组临界曲线。
NAV(6%)=28(1+y)+20(A/F,6%,5)-100(1+x)(A/P,6%,5)=O
NAV(8%)=28(1+y)+20(A/F,8%,5)-100(1+x)(A/p,8%,5)=O
NAV(10%)=28(1+y)+20(A/F,10%,5)-100(1+x)(A/P,10%,5)=0
NAV(12%)=28(1+y)+20(A/F,12%,5)-100(1+x)(A/P,12%,5)=0
NAV(15%)=28(1+y)+20(A/F,15%,5)-100(1+x)(A/P,15%,5)=0
NAV(20%)=28(1+y)+20(A/F,20%,5)-100(1+x)(A/P,20%,5)=0
即
y(6%)=0.8479x-0.2789
y(8%)=0.8946x-0.2271
y(10%)=0.9421x-0.1749
y(12%)=0.9907x-0.1217
y(15%)=1.0653x-0.0406
y(20%)=1.1943x-0.09829
将上面这些曲线绘在以x和Y为坐标的平面图上,即是图2。
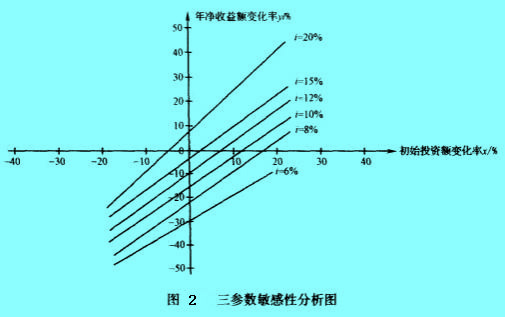
从图2可以看出,基准收益率i上升,临界线向上方移动,使净现值NAV>0的范围缩小,基准收益率降低;临界线向下方移动,使净现值NAV>O的区域扩大。根据这种三因素敏感性分析图,我们能够直观地了解投资额、年净收益和基准收益率这三个因素同时变动对项目经济效益的影响,有助于做出正确的决策。
