价格优化模型

1.价格优化模型简介

价格优化模型（PriceOptimizationModels）比较抽象,我们用收益管理来解读.原则是将合适的产品在合适的时间，以合适的价格销售给合适的顾客，并由此使企业在其产品中获得最大限度的收益。它以市场细分和需求预测为基础，一方面采取超售（通过超生产规模来接受订货）的方法来减少虚假订货带来的不必要的虚耗；另一方面采取存货控制的方法，将市场细分、需求预测和产品定价紧密结合，最大限度地适应市场需求的多样性，发掘产品在市场的获利潜力，实现收益的最大化。

2.Price Optimization Models[1]

Image:价格优化模型.jpg

25种最流行的管理工具

客户关系管理

全面质量管理

顾客细分

外包

核心能力

供应链管理

战略规划

业务流程再造

知识管理

使命书和企业愿景书

平衡记分卡

作业基础管理

忠诚度管理

六西格玛

战略联盟

基准管理

变革管理计划

增长战略

经济附加值增值分析

价格优化模型

开放市场创新

规模定制

情景设定和突发计划

海外经营

射频识别

[编辑]

Price Optimization Models are mathematical programs that calculate price elasticities, or how demand varies at different price levels, then combine that data with information on costs and inventory levels to recommend prices that will improve profits. Price Optimization Models simulate how customers will respond to price changes, supplementing managers’ instincts with data-driven scenarios. The insights help to forecast demand, develop pricing and promotion strategies, control inventory levels, and improve customer satisfaction.

3.Methodology[1]

To implement Price Optimization Models, practitioners should:

Select the preferred optimization model, determine the desired outputs and understand the required inputs;

Collect historical data—including product volumes, the company’s prices and promotions, competitors’ prices, economic conditions, product availability, and seasonal conditions as well as fixed and variable cost details;

Clarify the business’s value proposition and set strategic rules to guide the modeling process;

Load, run and revise the model;

Establish decision processes that incorporate modeling results without alienating key decision makers;

Monitor results and upgrade data input to continuously improve modeling accuracy.

4.Common Uses[1]

Price Optimization Models are used to determine initial pricing, promotional pricing and markdown (or discount) pricing.

Initial price optimization is well-suited to businesses that have a fairly stable base of products with long life cycles, such as grocery, chain drug, and office-supply stores, and manufacturers of commodities like packaging and tools.

Promotional price optimization helps businesses set temporary prices to spur sales of items with long life cycles, such as newly introduced products, products bundled together in special promotions and loss leaders.

Markdown optimization is well-suited to businesses that sell short life-cycle products that are subject to fashion trends and seasonality. Examples include service businesses like airlines and hotels, and certain kinds of specialty retailers, such as apparel retailers, mass merchants and big-box stores.

5.价格优化模型案例分析[2]

　　货物运输需求通常具有一定的派生性，这种派生性表现为市场对货物的需求并由此所决定的对货物的运输需要，因此，在建立货物运输价格模型时必须要考虑三个方面的因素，第一个方面，货物运输需求与这些货物的市场需求密切相关，货物运输需求量不可能大于这些货物的市场需求量；第二个方面，货物运输价格与货物的市场价格紧密相关，货物的运输价格需要与货物市场的价格保持一定的比例关系，为货物运输的用户留有一定的赢利空间，否则，这种派生的运输需求就有可能消失；第三个方面，货物运输企业必须要有一定的赢利，由于存在着多种运输方式，各种运输方式之间具有一定的可替代性，所以，这些运输方式为了追求和扩大各自的利益也存在着竞争。

　　如果将货物运输企业的利润简单地描述为运输收入与运输支出的差额，那么，可以建立货物运输企业的价格优化模型：

　　ob.maxπ = R(P(P_tl,P_qt),Q − C(Q)) (1)

　　st.P(P_tl,P_qt) < P_d(Q) (2)

　　其中：R(P,Q)表示收入函数，C(Q)表示支出函数，P(P_tl,p_qt表示运输价格函数，P_d(Q)表示市场价格函数，Q表示运量P_tl表示铁路运价，P_qt表示其他运输方式的运价。目标为在运输价格低于市场价格的约束下，使收入减支出最大。

　　对于有m种运输方式和n种运输货物的运输市场，建立价格优化模型：

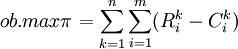　　 $ob.maxpi=sum^n_{k=1}sum^m_{i=1}(R^k_i-C^k_i)$ (3)

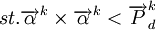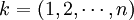
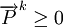
　　 $st.{overrightarrowalpha}^ktimes{overrightarrowalpha}^k<{overrightarrow P}^k_d$ (4)　　 $k=(1,2,cdots,n)$ 　　 $overrightarrow P^kge0$

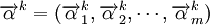　　 ${overrightarrowalpha}^k=({overrightarrowalpha}^k_1,{overrightarrowalpha}^k_2,cdots,{overrightarrowalpha}^k_m)$ (5)

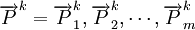　　 ${overrightarrow P}^k={overrightarrow P}^k_1,{overrightarrow P}^k_2,cdots,{overrightarrow P}^k_m$ (6)

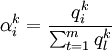　　 $alpha^k_i=frac{q^k_i}{sum^m_{t=1}q^k_l}$ (7)

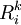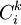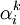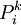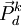　　其中： $R^k_i$ , $C^k_i$ 分别表示第k种货物通过第i种运输方式运输的收入和支出， $alpha^k_i$ 表示第i种运输方式运输的运量占该种货物各种运输方式总的运输量的比例， $P^k_i$ 表示第k种运输方式运输第i种货物的运价水平， $q^k_d$ 表示第k种货物通过第i种运输方式运输的运量， $vec{P}^k_d$ 表示第k种货物的市场价格水平。

　　为简化分析，设α^k为第k种货物各种运输方式的加权平均运价水平占该种货物的市场价格的比例，则式(4)可以表示为：

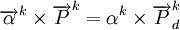
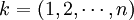　　 ${overrightarrowalpha}^ktimes{overrightarrow P}^k=alpha^ktimes{overrightarrow P}^k_d$ 　　 $k=(1,2,cdots,n)$ (8)

　　设γ_k为拉格朗日算子，构造函数：

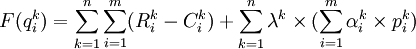　　 $F(q^k_i)=sum^n_{k=1}sum^m_{i=1}(R^k_i-C^k_i)+sum^n_{k=1}lambda^ktimes(sum^m_{i=1}alpha^k_itimes p^k_i)$ (9)

　　根据极值条件，有：

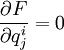　　 $frac{partial F}{partial q^i_j}=0$ 　（共i*j个方程）　　（10）

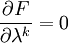　　 $frac{partial F}{partial lambda^k}=0$ 　（共k个方程）　　（11）

　　其中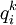 $q^k_i$ 之间存在如下关系：

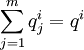　　 $sum^{m}_{j=1}q^i_{j}=q^i$ 　　（12）

　　并且，式（8）可以表示为：

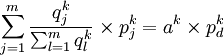　　 $sum^{m}_{j=1}frac{q^k_j}{sum^m_{l=1}q^{k}_{l}}times p^k_{j}=a^ktimes p^k_d$ 　　（13）

　　另外：

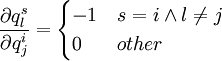　　 $frac{partial q^s_l}{partial q^i_j}=begin{cases}-1 & s=i land lne j 0 & otherend{cases}$ 　　（14）

　　根据价格弹性(e)定义，如果p(q)为价格，q为运量，R为收入，那么：

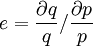　　 $e=frac{partial q}{q}/frac{partial p}{p}$ 　　（15）

　　并且，

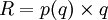　　 $R=p(q)times q$ 　　（16）

　　依式（15），（16）得式（17）：

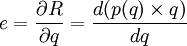
　　 $e=frac{partial R}{partial q}=frac{d(p(q)times q)}{dq}$

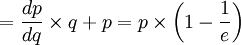　　 $=frac{dp}{dq}times q+p=ptimes left(1-frac{1}{e}right)$ 　　（17）

　　式中根据弹性的定义，为使e负。

　　将式（17）表示的结果运用到式（10）中，可以得到下式：

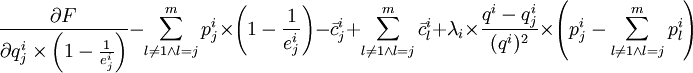　　 $frac{partial F}{partial q^i_{j}timesleft(1-frac{1}{e^i_j} right)}-sum^{m}_{lne 1land l=j} p^i_jtimesleft(1-frac{1}{e^i_j}right)-bar{c}^i_j+sum^{m}_{lne 1land l=j} bar{c}^i_{l}+lambda_itimesfrac{q^i-q^i_j}{(q^i)^2}timesleft(p^i_j-sum^m_{lne 1land l=j} p^i_{l}right)$ 　　（18）

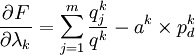　　 $frac{partial F}{partial lambda_k}=sum^{m}_{j=1}frac{q^k_j}{q^k}-a^ktimes p^k_{d}$ 　　（19）

　　由此，可以推导出通解（为简化分析，只考虑两种运输方式，即j = 1,2）

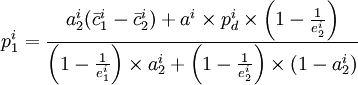　　 $p^i_1=frac{a^i_2(bar{c}^i_1-bar{c}^i_2)+a^itimes p^i_dtimes left(1-frac{1}{e^i_2}right)}{left(1-frac{1}{e^i_1}right)times a^i_2+left(1-frac{1}{e^i_{2}}right)times(1-a^i_2)}$ 　　（20）

　　其中：

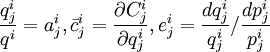　　 $frac{q^i_j}{q^i}=a^i_j,bar{c}^i_j=frac{partial C^i_j}{partial q^i_j},e^i_j=frac{dq^i_j}{q^i_j}/frac{dp^i_j}{p^i_j}$ ,

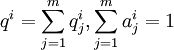
　　 $q^i=sum^{m}_{j=1}q^i_{j},sum^{m}_{j=1}a^i_{j}=1$

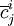　　 $overline{c}^i_j$ 表示j种运输方式i品类的边际成本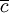， $overline{c}$ 表示其他各种运输方式的边际成本。式（20）可以变形为：

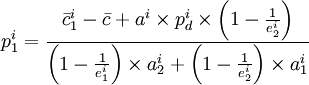　　 $p^i_1= frac{bar{c}^i_1-bar{c}+a^itimes p^i_{d}timesleft(1-frac{1}{e^i_2}right)}{left(1-frac{1}{e^i_1}right)times a^i_2+left(1-frac{1}{e^i_2}right)times a^i_1}$ 　（21）

　　由模型可以看出，对于某种品类的货物，运输价格主要与自身的边际成本、各种运输方式的综合边际成本、运价水平占货物市场价格的比例、货物的市场价格、各种运输方式的市场份额、货物的运输价格弹性以及其他运输方式的运输价格等因素有关。其中，边际成本与运输距离有关，价格弹性与价格有关，市场占有率与市场总需求量有关。

评论 | 0条评论

经理人分享